Arreglos
Todas las variables que se han considerado en las unidades anteriores son de tipo simple. Una variable de tipo simple consiste de una sola caja de memoria y sólo puede contener un valor cada vez. Una variable de tipo estructurado consiste en toda una colección de casillas de memoria. Los tipos de datos estudiados: entero, real, alfabético son considerados como datos de tipo simple, puesto que una variable que se define con alguno de estos tipos sólo puede almacenar un valor a la vez, es decir, existe una relación de uno a uno entre la variable y el número de elementos (valores) que es capaz de almacenar. En cambio un dato de tipo estructurado, como el arreglo, puede almacenar más de un elemento (valor) a la vez, con la condición de que todos los elementos deben ser del mismo tipo, es decir, que se puede tener un conjunto de datos enteros, reales, etc.
Datos estructurados:
Estructura de Datos es una colección de datos que se caracterizan por su organización y las operaciones que se definen en ella. Los datos de tipo estándar pueden ser organizados en diferentes estructuras de datos: estáticas y dinámicas.
Estructura de Datos estáticas:
Son aquellas en las que el espacio ocupado en memoria se define en tiempo de compilación y no puede ser modificado durante la ejecución del programa. Corresponden a este tipo los arrays y registros
Estructuras de Datos Dinámicas:
Son aquellas en las que el espacio ocupado en memoria puede ser modificado en tiempo de ejecución. Corresponden a este tipo las listas, árboles y grafos . Estas estructuras no son soportadas en todos los lenguajes. La elección de la estructura de datos idónea dependerá de la naturaleza del problema a resolver y, en menor medida, del lenguaje. Las estructuras de datos tienen en común que un identificador, nombre, puede representar a múltiples datos individuales.
Arrays:
Un arreglo (array) es una colección de datos del mismo tipo, que se almacenan en posiciones consecutivas de memoria y reciben un nombre común. Para referirse a un determinado elemento de un array se deberá utilizar un índice, que especifique su posición relativa en el array. Un arreglo es una colección finita, homogénea y ordenada de elementos. Finita:Todo arreglo tiene un límite; es decir,debe determinarse cuál será el número máximo de elementos que podrán formar parte del arreglo. Homogénea: Todos los elementos del arreglo deben ser del mismo tipo. Ordenada: Se puede determinar cuál es el primer elemento, el segundo, el tercero,.... y el n-ésimo elemento.
Los arreglos se clasifican de acuerdo con el número de dimensiones que tienen. Así se tienen los:
- Unidimensionales (vectores)
- Bidimensionales (tablas o matrices)
- Multidimensionales (tres o más dimensiones)
EjemploEstructura de Datos es una colección de datos que se caracterizan por su organización y las operaciones que se definen en ella. Los datos de tipo estándar pueden ser organizados en diferentes estructuras de datos: estáticas y dinámicas.
Estructura de Datos estáticas:
Son aquellas en las que el espacio ocupado en memoria se define en tiempo de compilación y no puede ser modificado durante la ejecución del programa. Corresponden a este tipo los arrays y registros
Estructuras de Datos Dinámicas:
Son aquellas en las que el espacio ocupado en memoria puede ser modificado en tiempo de ejecución. Corresponden a este tipo las listas, árboles y grafos . Estas estructuras no son soportadas en todos los lenguajes. La elección de la estructura de datos idónea dependerá de la naturaleza del problema a resolver y, en menor medida, del lenguaje. Las estructuras de datos tienen en común que un identificador, nombre, puede representar a múltiples datos individuales.
Arrays:
Un arreglo (array) es una colección de datos del mismo tipo, que se almacenan en posiciones consecutivas de memoria y reciben un nombre común. Para referirse a un determinado elemento de un array se deberá utilizar un índice, que especifique su posición relativa en el array. Un arreglo es una colección finita, homogénea y ordenada de elementos. Finita:Todo arreglo tiene un límite; es decir,debe determinarse cuál será el número máximo de elementos que podrán formar parte del arreglo. Homogénea: Todos los elementos del arreglo deben ser del mismo tipo. Ordenada: Se puede determinar cuál es el primer elemento, el segundo, el tercero,.... y el n-ésimo elemento.
Los arreglos se clasifican de acuerdo con el número de dimensiones que tienen. Así se tienen los:
- Unidimensionales (vectores)
- Bidimensionales (tablas o matrices)
- Multidimensionales (tres o más dimensiones)
Se quiere elaborar un programa que realice las siguientes acciones:
- Leer una lista de calificaciones de un examen
- Encontrar su media
- Escribir una lista de las calificaciones mayores que la media
- Ordenar la lista de las calificaciones en orden ascendente.
Supongamos también que hay 100 calificaciones. Debemos utilizar 100 variables diferentes nota1, nota2, ...., nota100, de ese modo son 100 direcciones diferentes de memoria para almacenar las calificaciones del examen. Te imaginas declarar las 100 variables, ¿cuántas instrucciones involucra?
Var Nota1,nota2,nota3,.........nota100: entero
(En la declaración real de un programa no pueden usarse puntos suspensivos, por lo tanto serán 100 veces) . En la fase de lectura de datos, serán también 100 veces las instrucciones para ir leyendo cada valor. Leer (nota1, nota2,nota3,........., nota100)
Para calcular la media:
Media = (nota1+nota2+.......+nota100)/100
Para la lista de calificaciones mayores que la media, deberá también irse comparando una por una:
Si nota1 > media entonces
escribir (nota1)
Fin_si
Si nota2 > media entonces
escribir (nota2)
Fin_si
Si nota100 > media entonces
escribir (nota100)
Fin_si
Y después de más de 450 líneas de código..... ¡Falta ordenar la lista de calificaciones en orden ascendente!
Después que aprendas a usar arreglos verás cómo se ahorra instrucciones porque es fácil recorrer toda la lista de notas con unas pocas instrucciones. En el caso anterior, cuando el acceso a la información es secuencial, sólo se puede acceder a un elemento buscando desde el principio de la lista, y esto es algo lento. Lo que se necesita es una estructura de acceso directo que permita almacenar y recuperar los datos directamente especificando su posición en la estructura, de esa manera se requerirá el mismo tiempo para acceder al elemento de la posición 100 que el de la posición 5.
También preferiremos que esta estructura se almacene en memoria principal para que su almacenaje y recuperación sea más rápida. Es por ello que existen los arreglos, que están organizados en una secuencia de elementos, todos del mismo tipo y se puede acceder a cada elemento directamente especificando su posición en esta secuencia.
Arreglos Unidimensionales:
Están formados por un conjunto de elementos de un mismo tipo de datos que se almacenan bajo un mismo nombre, y se diferencian por la posición que tiene cada elemento dentro del arreglo de datos. Al declarar un arreglo, se debe inicializar sus elementos antes de utilizarlos. Para declarar un arreglo tiene que indicar su tipo, un nombre único y la cantidad de elementos que va a contener. Por ejemplo, las siguientes instrucciones declaran tres arreglos distintos:
Para acceder a valores específicos del arreglo, se utiliza un valor de índice que apunte al elemento deseado. Por ejemplo, para acceder al primer elemento del arreglo calificaciones debe utilizar el valor de índice 0 (calificaciones[0]).
Inicialización y asignación de valores
Como se decía anteriormente, antes de utilizar un arreglo es necesario inicializarlo:
Calificaciones[0];
Para inicializar todos los elementos de una vez, se colocan dentro de una estructura for que va del primer elemento al último que contiene el arreglo. Para asignar un valor a un elemento del arreglo se hace por ejemplo:
Calificaciones[0] =100;
Cuando se usan arreglos, una operación común es usar una variable índice para acceder a los elementos de un arreglo. Suponiendo que la variable índice I contiene el valor 3, la siguiente instrucción asigna el valor 400 a valores[3]:
valores[I] = 400;
Partes de un arreglo:
Los componentes. Hacen referencia a los elementos que forman el arreglo, es decir, a los valores que se almacenan en cada una de las casillas del mismo. Los índices. Permiten hacer referencia a los componentes del arreglo en forma individual, especifican cuántos elementos tendrá el arreglo y además, de qué modo podrán accederse esos componentes.
Definición de Arreglos:
ident_arreglo = arreglo[limite_inf .. limite_sup] de tipo Operaciones con Vectores:
Las operaciones que se pueden realizar con vectores durante el proceso de resolución de un problema son:
- Lectura/ escritura
- Asignación
- Actualización(inserción, eliminación, modificación)
- Recorrido (acceso secuencial)
- Ordenación
- Búsqueda
Ejemplos:
Sea arre un arreglo de 70 elementos enteros con índices enteros. Su representación nos queda:
Ejemplos:
Sea bool un arreglo de 26 elementos booleanos con índices de tipo caracter. Su representación nos queda:
Bool = arreglo["a".."z"] de booleanos
Número total de elementos:
NTE= (ord("z")-ord("a")) + 1 = 122-97+1 = 26 elementos
Lectura
El proceso de lectura de un arreglo consiste en leer y asignar un valor a cada uno de sus elementos. Normalmente se realizan con estructuras repetitivas, aunque pueden usarse estructuras selectivas. Usamos los índices para recorrer los elementos del arreglo:
desde i = 1 hasta 70 hacer
leer ( arre[i])
fin_desde
Escritura:
Es similar al caso de lectura, sólo que en vez de leer el componente del arreglo, lo escribimos.
leer (N)
desde i = 1 hasta N hacer
escribir (arre[i])
fin_desde
Asignación:
No es posible asignar directamente un valor a todo el arreglo; sino que se debe asignar el valor deseado en cada componente. Con una estructura repetitiva se puede asignar un valor a todos los elementos del vector.
Por ejemplo:
arre[1] =120 (asignación de un valor constante único a una casilla del vector)
arre[3] = arre[1] / 4 (asignar una operación)
Se puede asignar un valor constante a todos los elementos del vector:desde i = 1 hasta 5 hacer
arre[i] = 3
fin_desde
O bien
arre = 3 (con arre del tipo arreglo)
Inicialización
Para inicializar con cero todos los elementos del arreglo:
desde i = 1 hasta 70 hacer
arre[i] = 0
fin_desde
Estructuras de datos y arreglos
NTE= (ord("z")-ord("a")) + 1 = 122-97+1 = 26 elementos
Lectura
El proceso de lectura de un arreglo consiste en leer y asignar un valor a cada uno de sus elementos. Normalmente se realizan con estructuras repetitivas, aunque pueden usarse estructuras selectivas. Usamos los índices para recorrer los elementos del arreglo:
desde i = 1 hasta 70 hacer
leer ( arre[i])
fin_desde
Escritura:
Es similar al caso de lectura, sólo que en vez de leer el componente del arreglo, lo escribimos.
leer (N)
desde i = 1 hasta N hacer
escribir (arre[i])
fin_desde
Asignación:
No es posible asignar directamente un valor a todo el arreglo; sino que se debe asignar el valor deseado en cada componente. Con una estructura repetitiva se puede asignar un valor a todos los elementos del vector.
Por ejemplo:
arre[1] =120 (asignación de un valor constante único a una casilla del vector)
arre[3] = arre[1] / 4 (asignar una operación)
Se puede asignar un valor constante a todos los elementos del vector:desde i = 1 hasta 5 hacer
arre[i] = 3
fin_desde
O bien
arre = 3 (con arre del tipo arreglo)
Inicialización
Para inicializar con cero todos los elementos del arreglo:
desde i = 1 hasta 70 hacer
arre[i] = 0
fin_desde
Estructuras de datos y arreglos
Acceso Secuencial. (Recorrido)
El acceso a los elementos de un vector puede ser para leer en él o para escribir (visualizar su contenido). Recorrido del vector es la acción de efectuar una acción general sobre todos los elementos de ese vector.
Actualización.
Incluye añadir (insertar), borrar o modificar algunos de los ya existentes. Se debe tener en cuenta si el arreglo está o no ordenado. Añadir datos a un vector consiste en agregar un nuevo elemento al final del vector, siempre que haya espacio en memoria.
Arreglo Bidimensional:
Es un conjunto de datos homogéneo, finito y ordenado, donde se hace referencia a cada elemento por medio de dos índices. El primero se utiliza para los renglones (filas) y el segundo para las columnas. También puede definirse como un arreglo de arreglos. Internamente en memoria se reservan MxN posiciones consecutivas para almacenar todos los elementos del arreglo.
El acceso a los elementos de un vector puede ser para leer en él o para escribir (visualizar su contenido). Recorrido del vector es la acción de efectuar una acción general sobre todos los elementos de ese vector.
Actualización.
Incluye añadir (insertar), borrar o modificar algunos de los ya existentes. Se debe tener en cuenta si el arreglo está o no ordenado. Añadir datos a un vector consiste en agregar un nuevo elemento al final del vector, siempre que haya espacio en memoria.
Arreglo Bidimensional:
Es un conjunto de datos homogéneo, finito y ordenado, donde se hace referencia a cada elemento por medio de dos índices. El primero se utiliza para los renglones (filas) y el segundo para las columnas. También puede definirse como un arreglo de arreglos. Internamente en memoria se reservan MxN posiciones consecutivas para almacenar todos los elementos del arreglo.
Const
M=valor1
N= valor2
Tipo
Array[1..M,1..N] de real:matriz
Var
Matriz:A
Desde i = 1 hasta M hacer
Desde j = 1 hasta N hacer
Escribir (A[i,j])
Fin_desde
Fin_desde
El recorrido por columnas se hace de manera similar, invirtiendo el sentido de los índices.
Desde j = 1 hasta N hacer
Desde i = 1 hasta M hacer
Escribir (A[i,j])
Fin_desde
Fin_desde
El número de elementos que contendrá una fila viene dado por U1-L1+1 (Valor mayor - valor menor +1). Igualmente, el número de elementos para la columna es U2-L2+1. Así, el número total de elementos de la tabla es (U2-L2+1)*(U1-L1+1)
Ejemplos.
1) Rellenar una matríz identidad de 4 por 4 elementos.
Una matriz identidad es aquella en la que la diagonal principal está llena de unos y el resto de los elementos son cero. Para llenar la matriz identidad se debe verificar que cuando los índices i y j sean iguales, la posición vale 1, en caso contrario se asigna cero al elemento i,j.







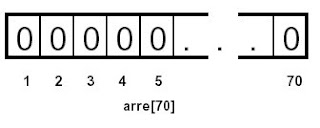


No hay comentarios:
Publicar un comentario